24® Game Classroom Activities
Activity—Grouping skills
Editions used: Add/Subtract; Multiply/Divide; Fractions Primer (2 Dot and 3 Dot cards)
The example below uses a Multiply/Divide 2 Dot card. (You can do this activity with Add/Subtract cards, using only addition and subtraction.) The purpose of this activity is to encourage students to practice grouping skills.
Select a card and draw the two wheels and the target number on the board. Ask a student to choose a wheel, then choose two numbers from that wheel. Write the two numbers on the board four times, with a space for the operation sign.
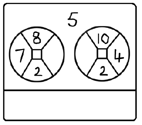
Example: The numbers 8 and 2 are chosen from the left wheel.
Ask: What operations can I use?
Ask: What will be the answer for the first equation?
8 + 2 = 10
8 – 2 = 6
Change the 8 to a 7.
8 x 2 = 16
8 ÷ 2 = 4
Ask: With the 10 we made, and with the number 7 remaining on the wheel, can we make a 5? (No.) Let’s try another equation.
Ask: With the 6 we made, and the number 7 remaining on the wheel, can we make a 5? (No.) Let’s try another equation.
Ask: With the 16 we made, and with the number 7 remaining on the wheel, can we make a 5? (No.) Let’s try the another equation.
Ask: With the 4 we made, and the number 7 remaining on the wheel, can we make a 5? (No.) Because those equations did not work, let’s try two other numbers on this wheel.
When doing this activity with Multiply/Divide Primer cards, have the class cycle through all the pairs of numbers on one wheel before moving on to the other wheel. Then, repeat the activity using two numbers from the other wheel.
Example:
4 + 2 = 6
4 – 2 = 2
4 x 2 = 8
4 ÷ 2 = 2
Ask: With the 6 we made, and with the 10 remaining on the wheel, can we make a 5? (No.) Let’s try another equation.
Ask: With the 2 and the 10 remaining on the wheel, can we make a 5? (Yes.) Someone tell me how.
10 ÷ 2 = 5
Ask: Can someone tell me all the steps to solve this card?
4 – 2 = 2 10 ÷ 2 = 5
NOTE: Sometimes students will pick the correct answer first and it will not be necessary to work through different equations. However, it is recommended that students see at least one example where producing many equations must be attempted to obtain a correct answer. Cycling through the possibilities helps students begin to recognize patterns. This process helps students learn to eliminate combinations that will not work because the number created is too large, too small, or in the case of a division problem, does not divide evenly. Encourage students to discuss (or write about) unrealistic answers and why they do not need to be considered.

